Correct answers 1 question Analyze the graph of the function f(x) to complete the statement on a coordinate plane, a curved line, labeled f of x, with a minimum value of (0, negative 3) and a maximum value of (negative 24, 17), crosses the xaxis at (negative 3, 0), (negative 11, 0), and (09, 0), and crosses the yaxis at (0, negative 3) f(x)< 0 over (∞,3) and what other intervalStack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeConfidence Intervals This chapter continues our study of estimating population parameters from random samplesIn we studied estimators that assign a number to each possible random sample, and the uncertainty of such estimators, measured by their RMSE (The RMSE is the squareroot of the expected value of the squared difference between the estimator and the parameter—a
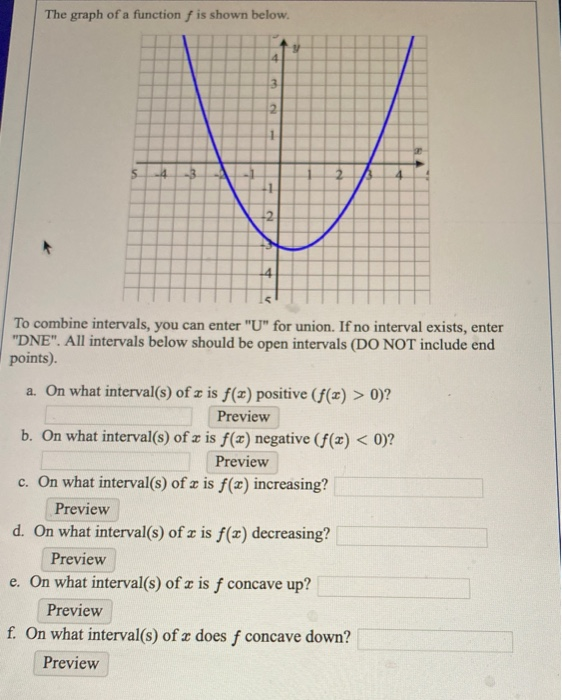
The Graph Of A Function F Is Shown Below To Combine Chegg Com
What is f(–2) quizlet
What is f(–2) quizlet-Now that we have explored derivatives, we can begin to assess what f' and f'' say about f You may already have recognized some properties of first and second derivatives, but here we will lay them all out The following statements are true a) If f'(x) >0 on an interval, then f is increasing on that intervalThat we know an interval a,b on which f(x) changes sign If f(x) is actually a continuous mathematical function, then there must be a point x∗ somewhere in the interval where f(x∗) = 0 But the notion of continuity does not strictly apply to floatingpoint computation We might not be able to actually find a point where f(x) is exactly




A 1 On What Interval S Is The Function F X 5 Chegg Com
Free math problem solver answers your algebra homework questions with stepbystep explanations1, for x = 0 Solution For all intervals of x other than when it is equal to 0, f(x) = 2x (which is a linear function) To graph the linear function, we can use two points to connect the line Just make sure that the two points satisfy y = 2x Make sure to leave the point of origin unfilledF(x) t 0 for all x , d ³ b p a x b a) dx 1 and ³ ff) dx 1 The support of a continuous random variable is the smallest interval containing all values of x where f(x) >= 0 Remark A crucial property is that, for any real number x, we have P(X x) 0 (implying there is no difference between Xdx) and X x));
Interval halving a midpoint c is calculated as the arithmetic mean between a and b, c = (a b) / 2;If the graph of f is a parabola with vertex on x axis and opening up, then the range of f is given by the interval 0 , infinity) The graph of f(x 5) is that of f(x) shifted 5 units to the right and therefore no change to the range If one opens up the other opens downCalculus Graphing with the First Derivative Identifying Turning Points (Local Extrema) for a Function 1 Answer
Get an answer for 'Determine the intervals on which the function f(x)=x^x defined on the interval (0,∞) is decreasing and increasing' and find homework help for other Math questions at eNotesAnswer to 48 Identify the intervals on which f'(x) > 0 (The Get an answer for '`f(x) = x/(x^2 1)` (a) Find the intervals on which `f` is increasing or decreasing (b) Find the local maximum and minimum values of `f
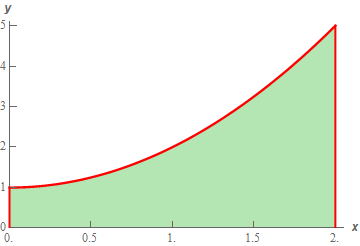



Calculus I Area Problem
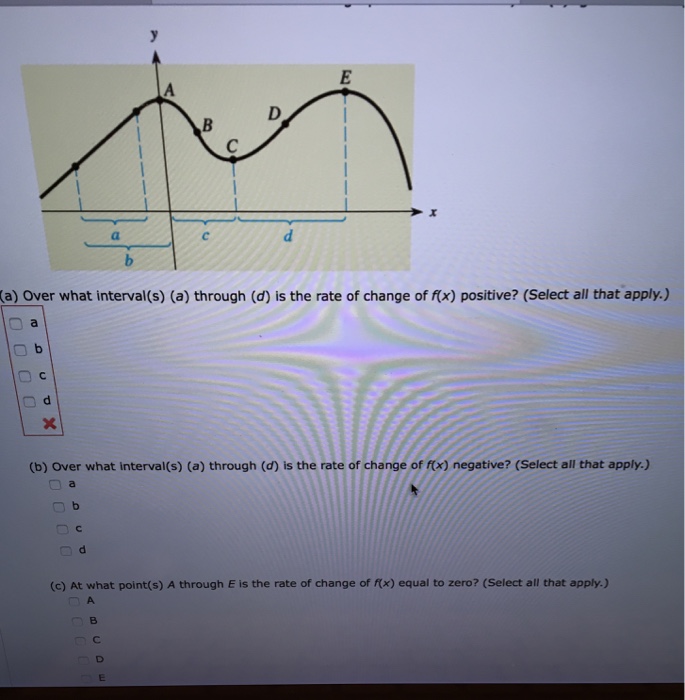



Answered P B A Over What Interval S A Bartleby
For each of the following functions, verify that the function satisfies the criteria stated in Rolle's theorem and find all values \(c\) in the given interval where \(f'(c)=0\) \(f(x)=x^22x\) over \(−2,0\) \(f(x)=x^3−4x\) over \(−2,2\) Solution Since \(f\) is a polynomial, it is continuous and differentiable everywhereThe function f is evaluated for the value of c if f(c) = 0 means that we found the root of the function, which is c6041/6431 Spring 08 Quiz 2 Wednesday, April 16, 730 930 PM SOLUTIONS Name Recitation Instructor TA Question Part




Analyzing Tables Flashcards Quizlet
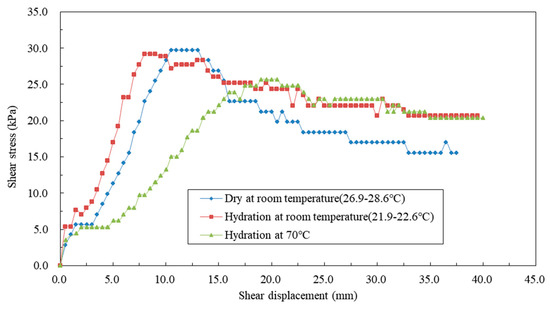



Sustainability April 2 21 Browse Articles
On the graph of a line, the slope is a constant The tangent line is just the line itself So f' would just be a horizontal line For instance, if f (x) = 5x 1, then the slope is just 5 everywhere, so f' (x) = 5 Then f'' (x) is the slope of a horizontal linewhich is 0 So f'' (x) = 0 See if you can guess what the third derivative is, or1/2 1/2 t f (t) = rect(t) If x(t) ,X(f), then X(t) ,x(f) In other words, FFx(t) = x(t) The Fourier transform of a sine or cosine at a frequency f 0 only has energy exactly at f 0, which is what we would expect Cu (Lecture 7)0 where x is the number Note that average velocity is found over a time interval Instantaneous velocity is usually called velocity, and it can be found at any time x, as follows We can, of course, use variables other than x and y to represent functions and their derivatives
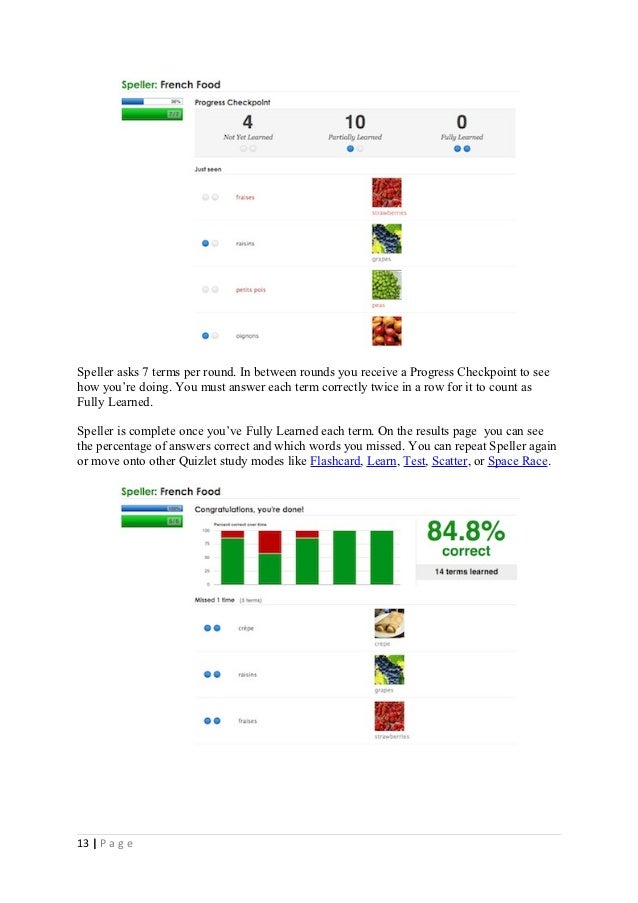



Using Quizlet
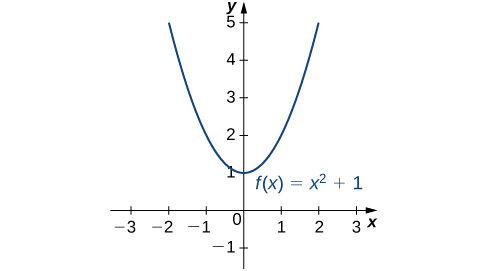



4 3 Maxima And Minima Calculus Volume 1
Or*probability(density(function(pdf)of*X isa*function* f(x) such*that*for*anytwo*numbers a and b with* a ≤ b , we*have The*probabilitythat* X is in*the*interval* a , b *can*be*F(x) > 0 over the interval (–infinity, 3) f(x) > 0 over the interval (–infinity, infinity) f(x) < 0 over the interval (–infinity, 3) f(x) < 0 eeduanswerscomSummary "Function Composition" is applying one function to the results of another (g º f) (x) = g (f (x)), first apply f (), then apply g () We must also respect the domain of the first function Some functions can be decomposed into two (or more) simpler functions



1



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q5 Pdf
The known derivatives of the elementary functions x 2, x 4, sin(x), ln(x) and exp(x) = e x, as well as the constant 7, were also used Definition with hyperreals Relative to a hyperreal extension R ⊂ ⁎ R of the real numbers, the derivative of a real function y = f ( x ) at a real point x can be defined as the shadow of the quotient ∆ y / ∆ x for infinitesimal ∆ x , where ∆ y = fFor a given function f(x),the Bisection Method algorithm works as follows two values a and b are chosen for which f(a) > 0 and f(b) < 0 (or the other way around);Fourier series over an interval T, T!




What Is The Average Rate Of Change In F X Over The Interval 4 13 A 1 3 B 4 13 C 11 13 D 11 8 Brainly Com
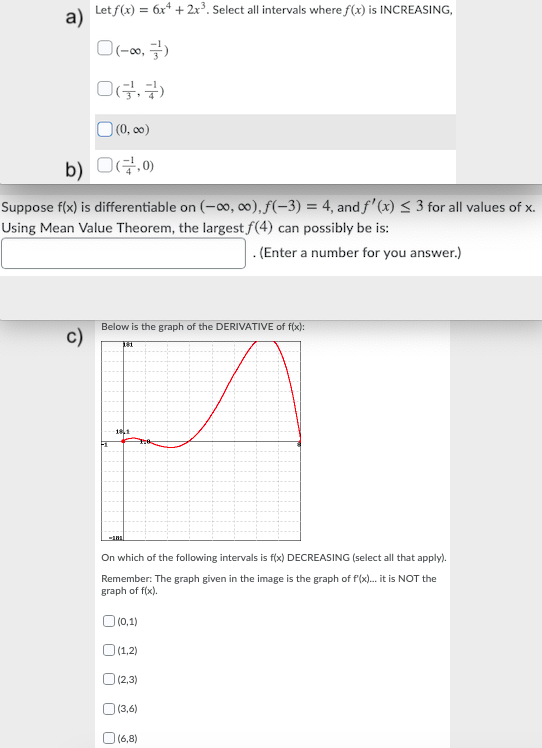



A Let F X 6x4 2x Select All Intervals Where Chegg Com
While some functions are increasing (or decreasing) over their entire domain, many others are not A value of the input where a function changes from increasing to decreasing (as we go from left to right, that is, as the input variable increases) is called a local maximumIf a function has more than one, we say it has local maximaCorrect answers 2 🔴 question What is the average rate of change for the function f(x) = x^27x4 over the interval (0,2)The theorem implies that there is at least one x 0 x_0 x 0 such that f (x 0) = y 0, f(x_0) = y_0, f (x 0 ) = y 0 , but there may be more than one, depending on f f f and y 0 y_0 y 0
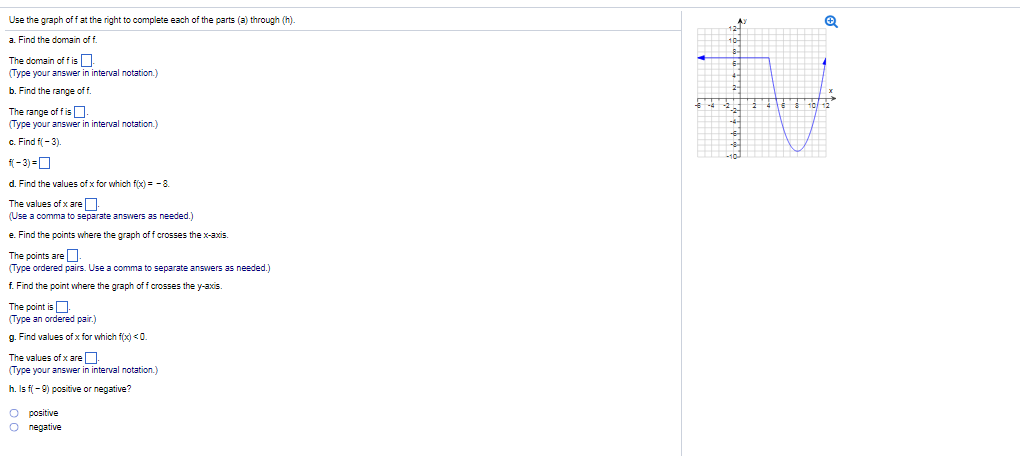



Use The Graph Of F At The Right To Complete Each Of Chegg Com



Graphing Rational Functions 2 Video Khan Academy
The function f in the following figure has an inflection point at cFor x between a and c, the value of f"(x) is negative, and for x between c and b, it is positive x → a c b f (x) Concave production function (z = input, f (z) = output) Note that some authors, including Sydsæter and Hammond (1995) (p 308), give a slightly different definition, in which the conditions f"(x) > 0 and f"(x f is a polynomial so f is continuous on the interval 0,3 f(0) = 2 and f(3) = 19 4 is between f(0) and f(3) so IVT tells us that there is a c in (0,3) with f(c) = 4 Finding the c requires solving x^3x^2x2 = 4 Which is equivalent to x^3x^2x6 = 0 Possible rational zeros are 1, 2, 3, and 6 Testing shows that 2 is a solution So c = 2Solution for Find the intervals where f"(x) < 0 or f"(x) > 0 as indicated f"(x) < 0 (1, 0) O (1, 0) (00, 1) (1, 0), (1, o0) Q Find explain and find the values of the trigonometric functions of θ from the information given cos A It is given that Since, both cos and tan trigonometric ratios are negative, the angle must lie in



Using Quizlet



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap17 Calculus Ab Q3 Pdf
0 energy points Math is a symbol for the logical symbol for there exists there exists an absolute absolute absolute maximum value value of f of F over interval over interval and minimum value when X is equal to C that's that right over here our maximum value when f is equal to D and for all the other X's in the interval we areUsing only the values given in the table for the function, f (x), what is the interval of xvalues over which the function is increasing?17 Transformations 123 2 to all of the xvalues of the points on the graph of y= f(x) to e ect a shift to the right 2 units Generalizing these notions produces the following result




Calculus Find The Average Rate Of Change Of A Function On Youtube
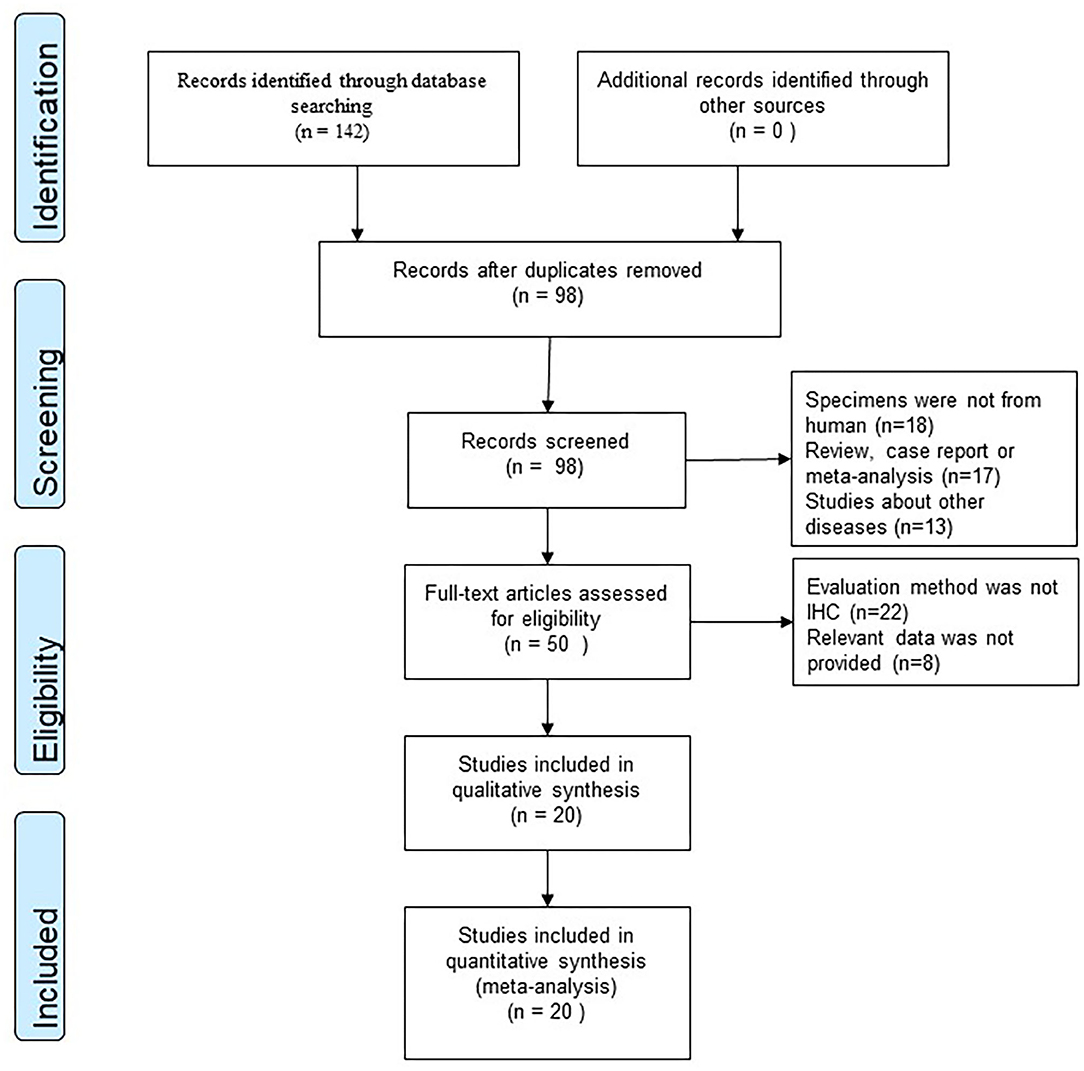



Frontiers Clinical Symptom Differences Between Mild And Severe Covid 19 Patients In China A Meta Analysis Public Health
Consider F(x)= cos 2x 2cos x over one complete period beginning with x = 0 a Find all values of x in this period at which F(x) = 0 b Find all values of x in this period at which the function has a minimum Justify your answer c Over what intervals in this period is the curve concave up?That is it is not possible to talk aboutApproximate the area under the graph of {eq}f(x) = x^23 {/eq} over the interval {eq}0,5 {/eq} by dividing the interval into 5 sub intervals and using the left endpoint of each sub interval
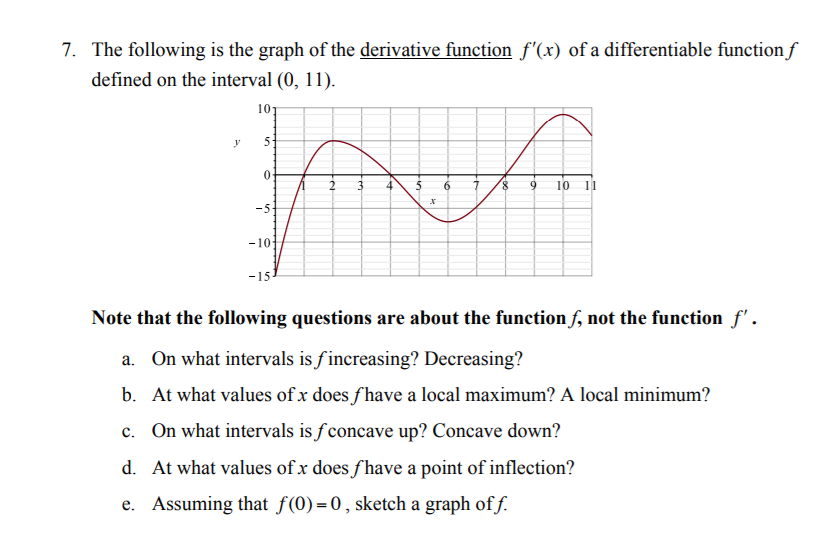



7 The Following Is The Graph Of The Derivative Chegg Com



1
) f(x k) k 1, 2, (1) It is convenient to introduce the probability function, also referred to as probability distribution, given by P(X x) f(x) (2) For x x k, this reduces to (1) while for other values of x, f(x) 0 In general, f(x) is a probability function if 1 f(x) 0 2 where the sum in 2 is taken over all possible values of x a x f ProblemSolving Strategy Calculating a Limit When \(f(x)/g(x)\) has the Indeterminate Form \(0/0\) First, we need to make sure that our function has the appropriate form and cannot be evaluated immediately using the limit laws We then need to find a function that is equal to \(h(x)=f(x)/g(x)\) for all \(x≠a\) over some interval containing aThe cumulative distribution function is therefore a concave up parabola over the interval \(1




Ap Calculus Chapter 3 7 Review Flashcards Quizlet




Answered Use The Graph Of F To Determine Each Of Bartleby
Find the absolute extrema of the given function #f(x)= sinxcosx# on interval #0,2pi#? 👍 Correct answer to the question Which statement is true about the given function?Definition A sequence of functions fn X → Y converges uniformly if for every ϵ > 0 there is an Nϵ ∈ N such that for all n ≥ Nϵ and all x ∈ X one has d(fn(x), f(x)) < ϵ Uniform convergence implies pointwise convergence, but not the other way around For example, the sequence fn(x) = xn from the previous example converges pointwise




The Graph Of A Function F Is Shown Below To Combine Chegg Com




Which Table Shows A Function That Is Increasing Only Over The Interval 2 1 And Nowhere Brainly Com
Click here 👆 to get an answer to your question ️ If f(x) = 3 – 2x and g (x) = StartFraction 1 Over x 5 EndFraction, what is the value of (StartFraction f Ov(3, 1) What ordered pair is closest to a local minimum of the function, f (x)? Note that the x 0 x_0 x 0 guaranteed by the theorem may not be unique;




Analyzing Graphs Flashcards Quizlet




Finding Increasing Interval Given The Derivative Video Khan Academy
View MATH110 WEEK 5 TESTdocx from MATH 110 at American Military University Summary Results Questions Correct 14 / Score 70% Full ResultsF(x) > 0 over the interval (∞, 4) What are the xintercepts of the graphed OTHER SETS BY THIS CREATOR Evaluating Logs (No Calculator) 31 terms MsColeMCS Analyzing Graphs 22 terms MsColeMCS Compound Interest 10 terms MsColeMCS Exponential Growth 9 terms MsColeMCS OTHER QUIZLET SETS Exam 4 questions 47 terms angelaraez95Fcontour (f) plots the contour lines of the function z = f (x,y) for constant levels of z over the default interval 5 5 for x and y example fcontour (f,xyinterval) plots over the specified interval To use the same interval for both x and y , specify xyinterval as a




Determine Whether The Following Statements Are True Chegg Com




Bacteria Use Collective Behavior To Generate Diverse Combat Strategies Sciencedirect
(2, 1) A local maximum of the function f (x) occurs when x = ___ 1




The Rate Of Change Of A Function
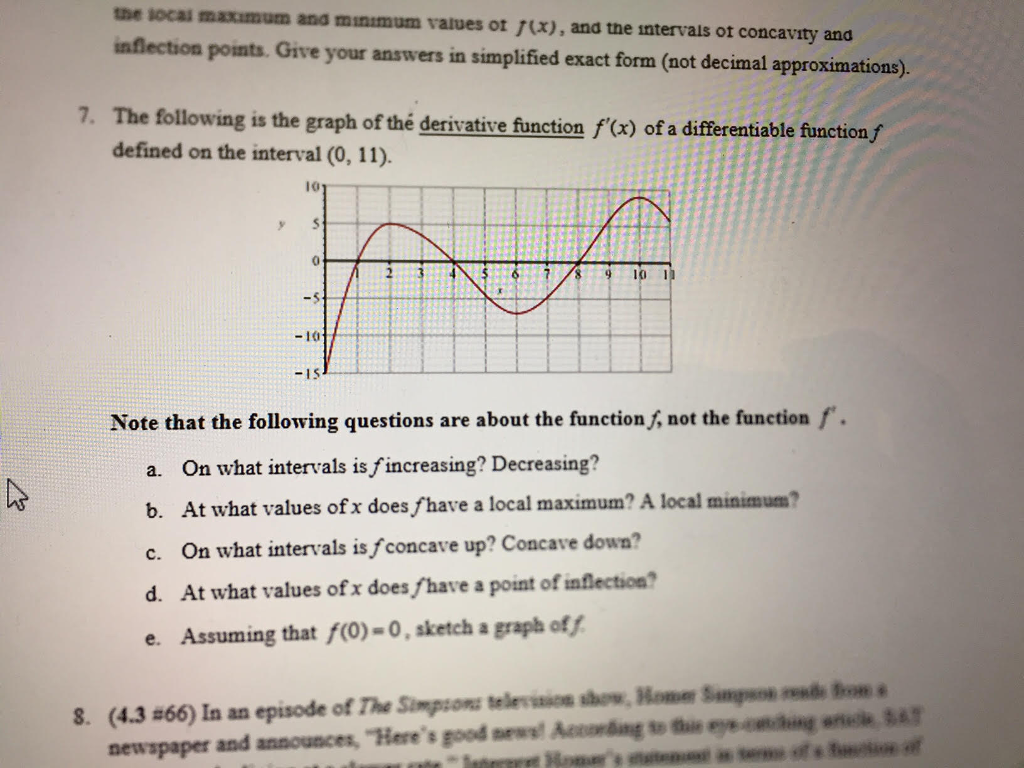



7 The Following Is The Graph Of The Derivative Chegg Com
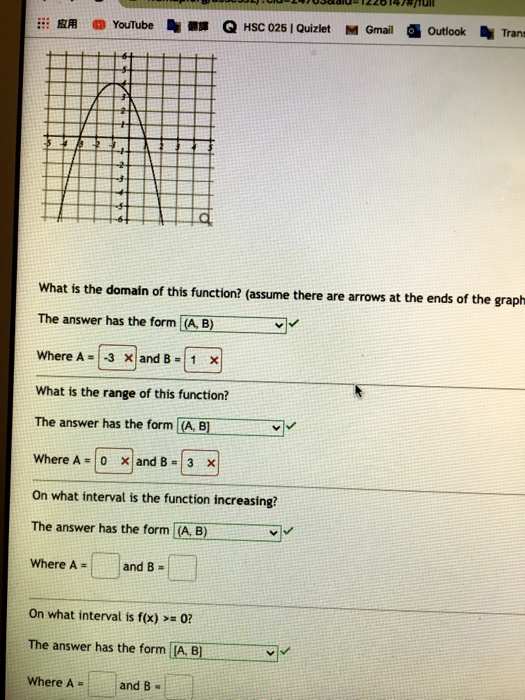



Youtube 3 Hsc 025 Quizlet M Gmail Outlook Trans Chegg Com




Analyzing Tables Flashcards Quizlet
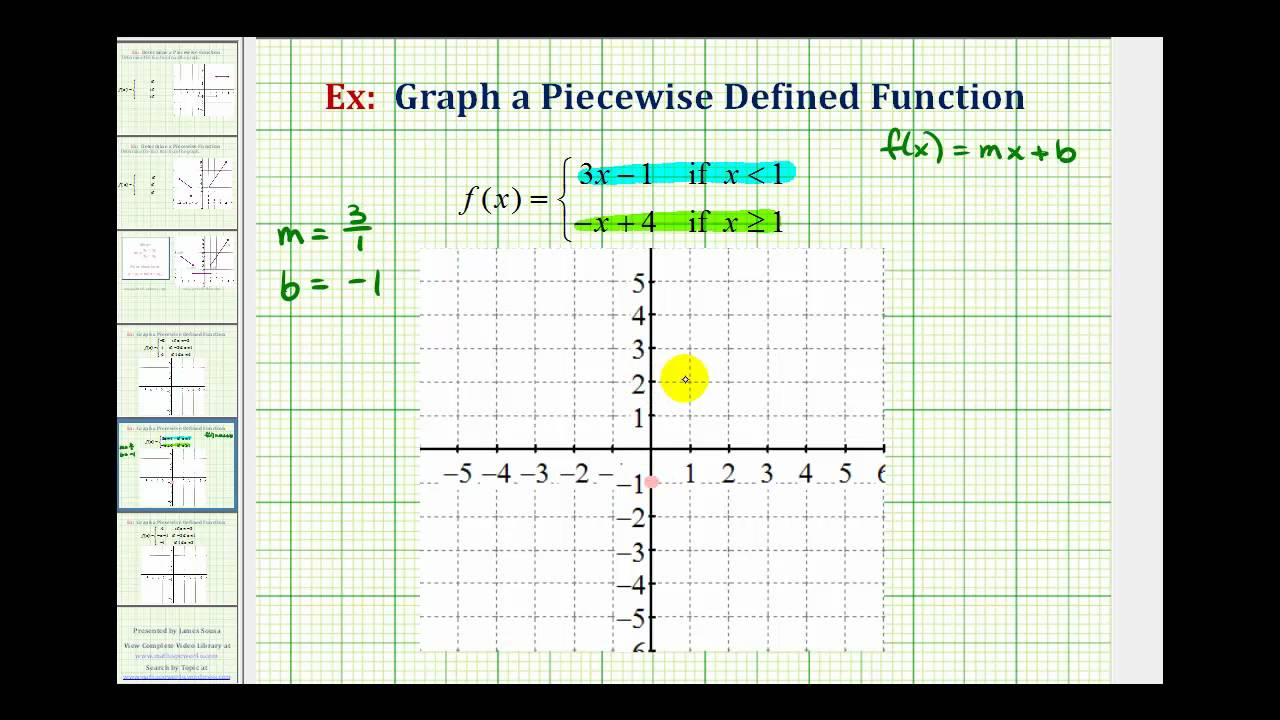



Graph Piecewise Defined Functions College Algebra




Analyzing Graphs Flashcards Quizlet
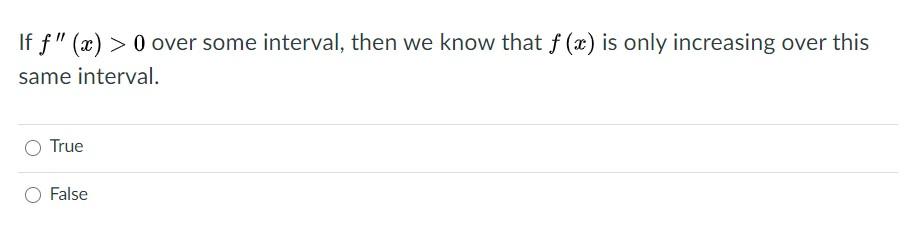



If F X 0 Over Some Interval Then We Know That F Chegg Com




Match The Conditions F X 0 And F 0 On A B With Chegg Com



Use The Remainder Estimation Theorem To Find An Interval Con Quizlet




Analyzing Graphs Flashcards Quizlet



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q5 Pdf




Using Quizlet



Www Tandfonline Com Doi Pdf 10 1080
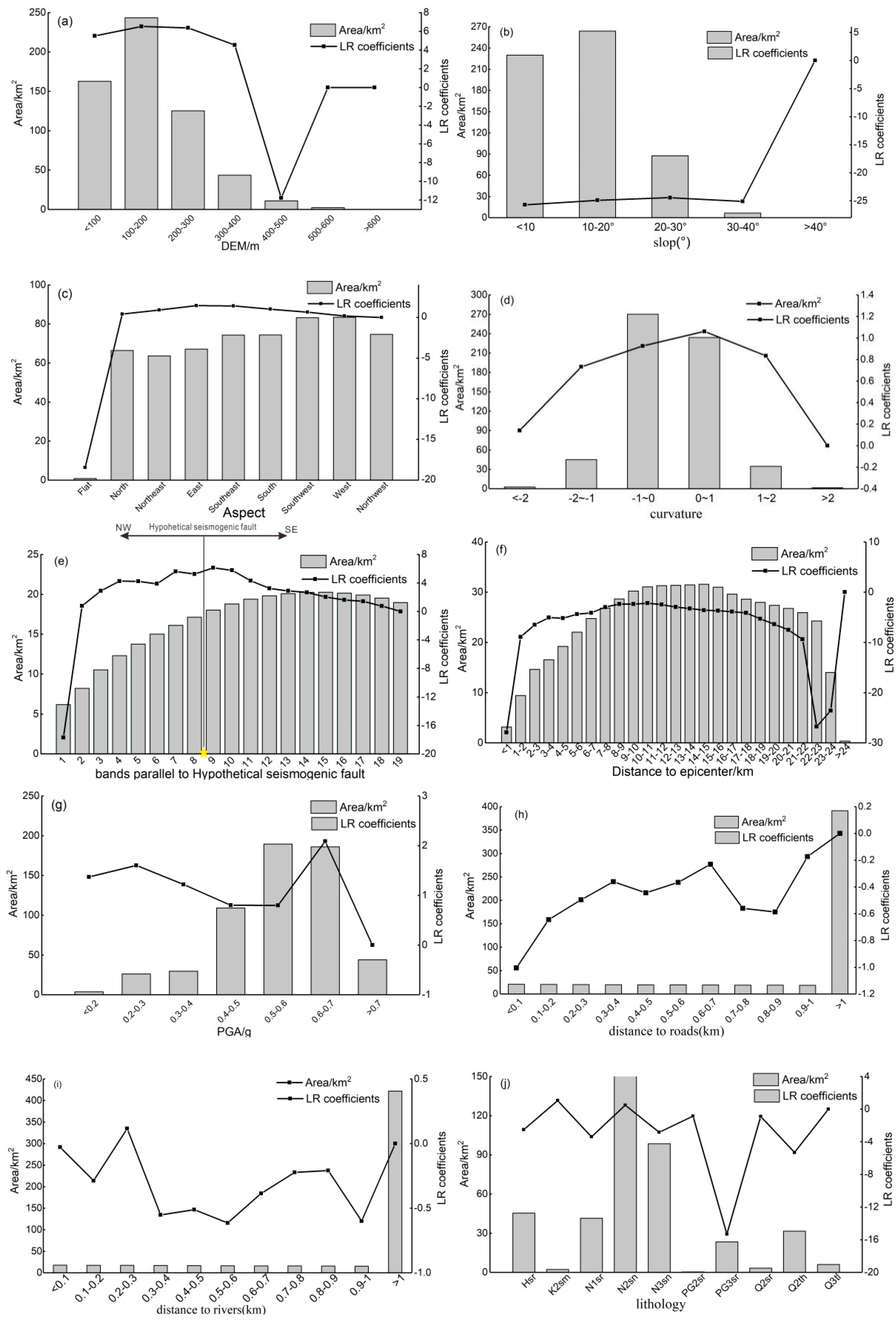



Remote Sensing Free Full Text Planet Image Based Inventorying And Machine Learning Based Susceptibility Mapping For The Landslides Triggered By The 18 Mw6 6 Tomakomai Japan Earthquake Html



Sustainability July 2 21 Browse Articles
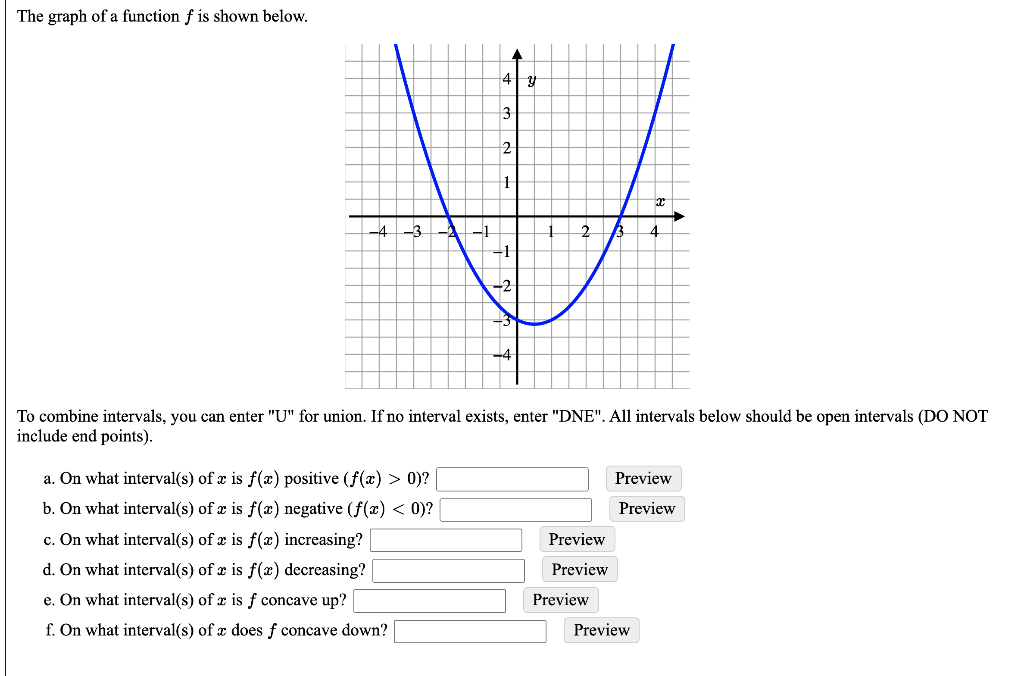



The Graph Of A Function F Is Shown Below 4 Y 3 2 1 2 Chegg Com



Energies Free Full Text Analysis And Modeling For Short To Medium Term Load Forecasting Using A Hybrid Manifold Learning Principal Component Model And Comparison With Classical Statistical Models Sarimax Exponential Smoothing And




North American Birds Require Mitigation And Adaptation To Reduce Vulnerability To Climate Change Biorxiv




Undergraduate Physiology Pecop Blog



Q Tbn And9gcsem Dcazkoagnoin0cupakjcwkxvggtudraf2y Usqp Cau
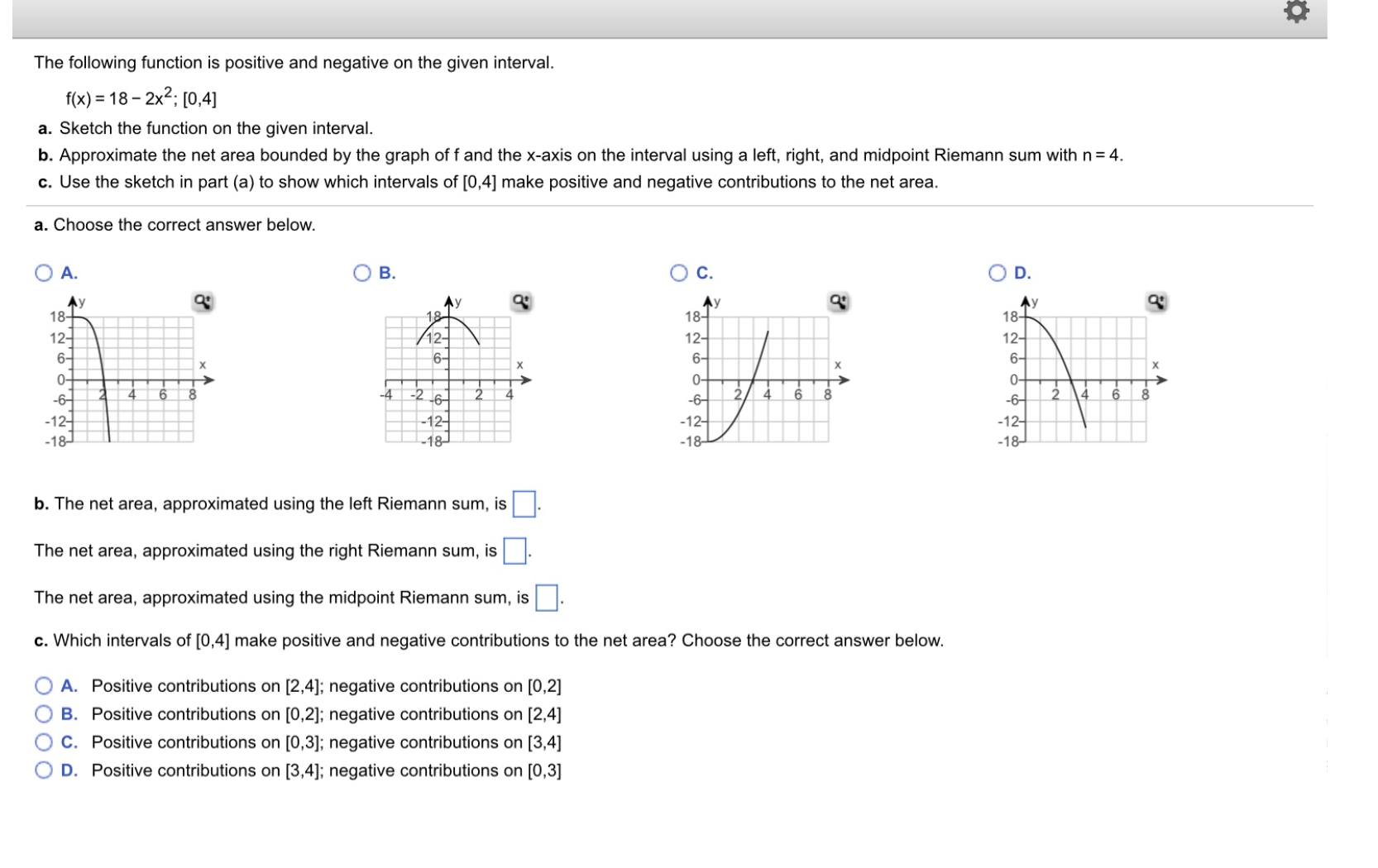



The Following Function Is Positive And Negative On Chegg Com




Analyzing Tables Flashcards Quizlet




Which Intervals Show F X Decreasing Check All That Apply Brainly Com




Distribution Behaviour Bioavailability And Remediation Of Poly And Per Fluoroalkyl Substances Pfas In Solid Biowastes And Biowaste Treated Soil Sciencedirect




Analyzing Tables Flashcards Quizlet




Using Quizlet To Begin Math Class Ap Calculus Calculus Studying Math




The Rate Of Change Of A Function




Theranostic Nanomedicine For Synergistic Chemodynamic Therapy And Chemotherapy Of Orthotopic Glioma Tan Advanced Science Wiley Online Library



Analyzing Tables Flashcards Quizlet




Killifish Eggs Can Disperse Via Gut Passage Through Waterfowl Silva 19 Ecology Wiley Online Library
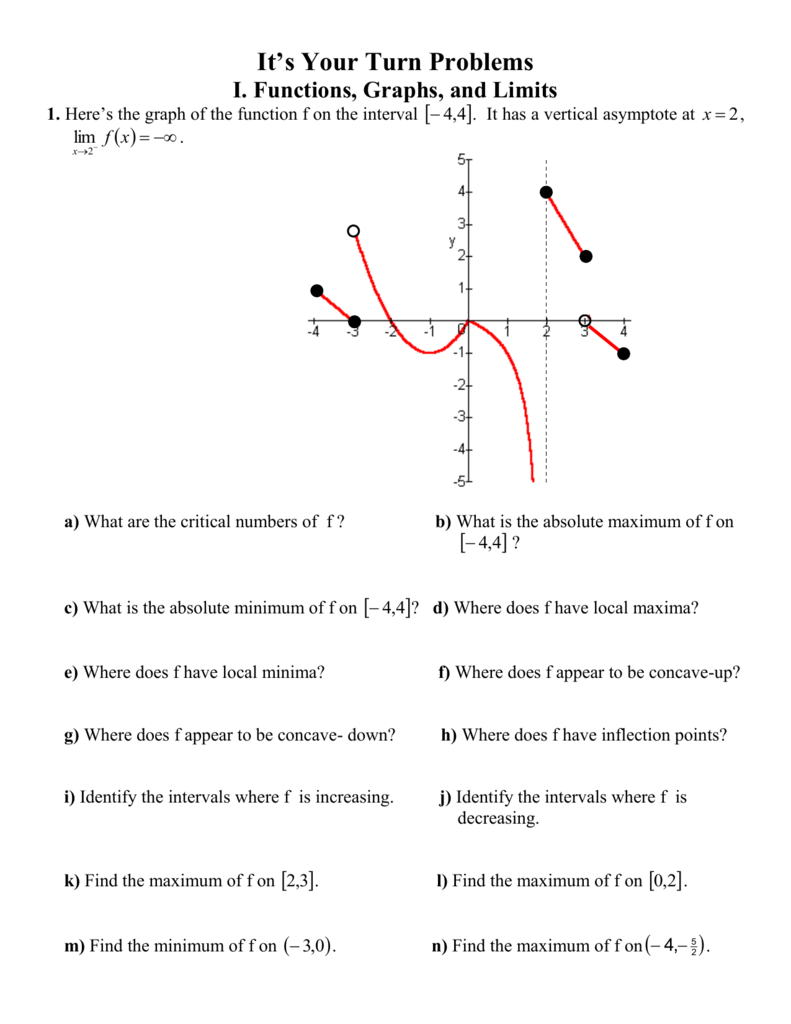



Doc Houston Area Calculus Teachers




Analyzing Graphs Flashcards Quizlet
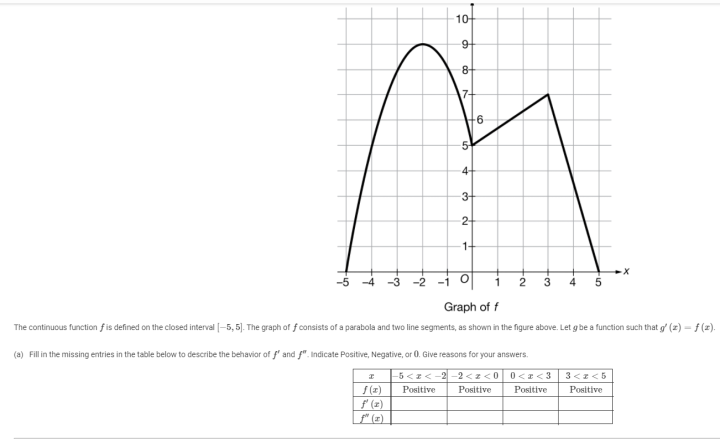



10 9 8 7 6 5 4 3 2 1 X 3 0 1 2 3 4 5 Graph Off Chegg Com




Curve Sketching F X



Curve Sketching F X




Analyzing Tables Flashcards Quizlet
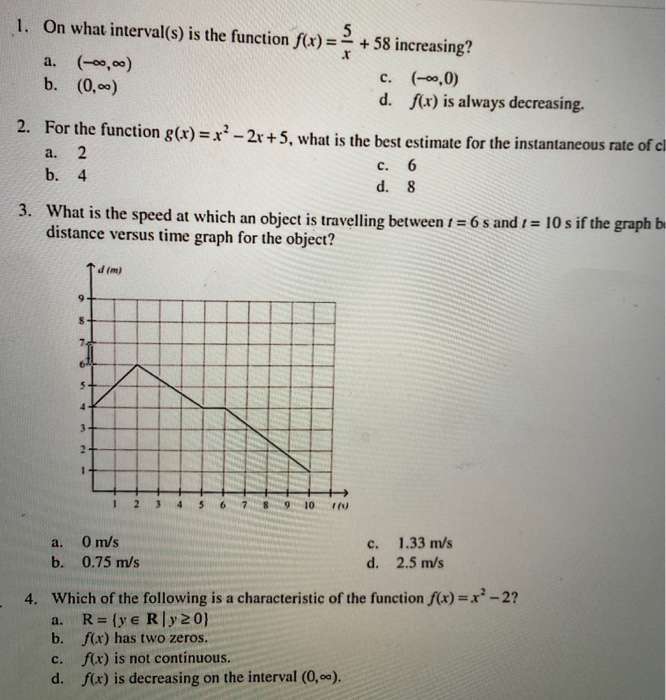



A 1 On What Interval S Is The Function F X 5 Chegg Com




Use The Graphing Tool To Determine The True Statements Regarding The Represented Function Check All Brainly Com
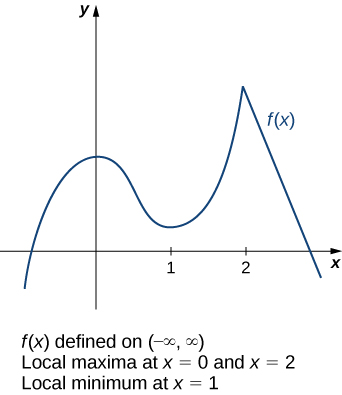



4 3 Maxima And Minima Calculus Volume 1
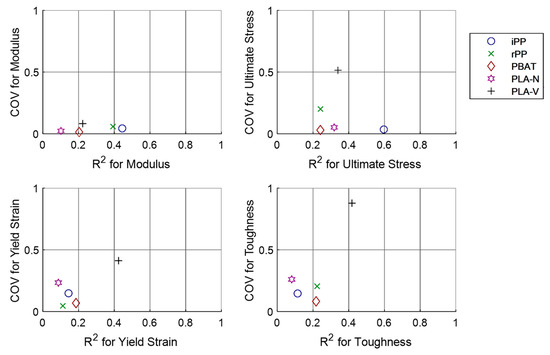



Sustainability July 2 21 Browse Articles




Finding Average Rate Of Change Of Polynomials Video Khan Academy




F X Lt 0 Over 3 And What Other Interval O 2 4 1 1 O 3 1 1 O 1 1 2 O 1 1 Brainly Com
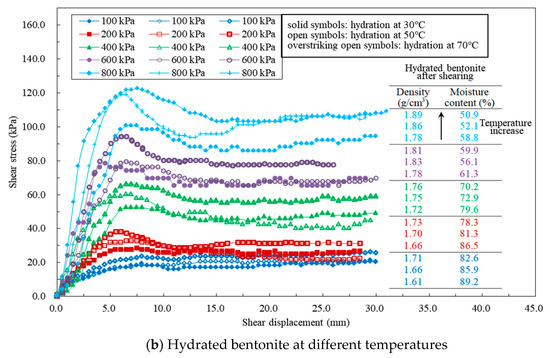



Sustainability April 2 21 Browse Articles




Which Statement Is True About The Graphed Function F X Lt 0 Over The Intervals 0 7 And Brainly Com
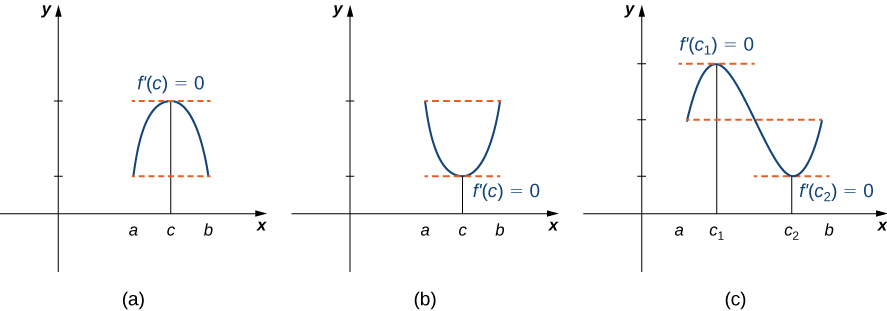



4 4 The Mean Value Theorem Calculus Volume 1




Which Statement Is True About The Given Function A F X Lt 0 Over The Intervals Infinity 2 7 Brainly Com
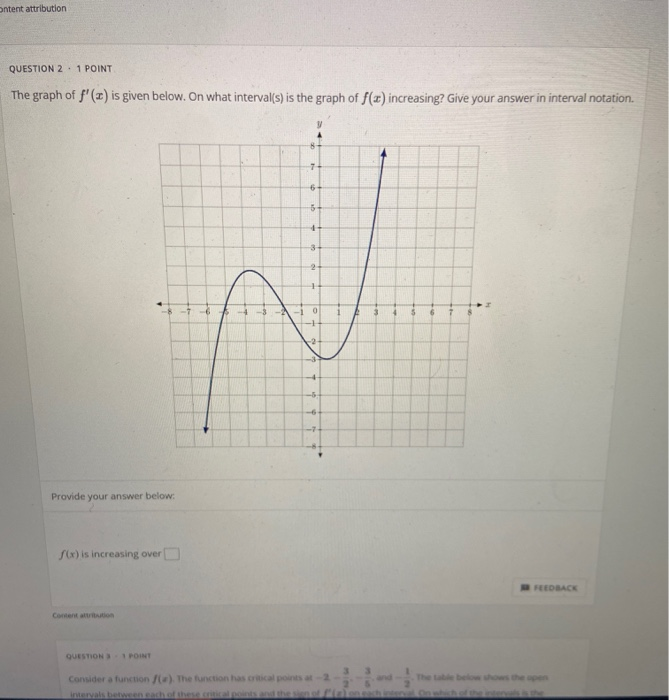



10 Hours C Question 1 1 Point The Graph Of F Is Chegg Com



Sustainability July 2 21 Browse Articles




Introduction To Quadratic Functions Assignment Flashcards Quizlet
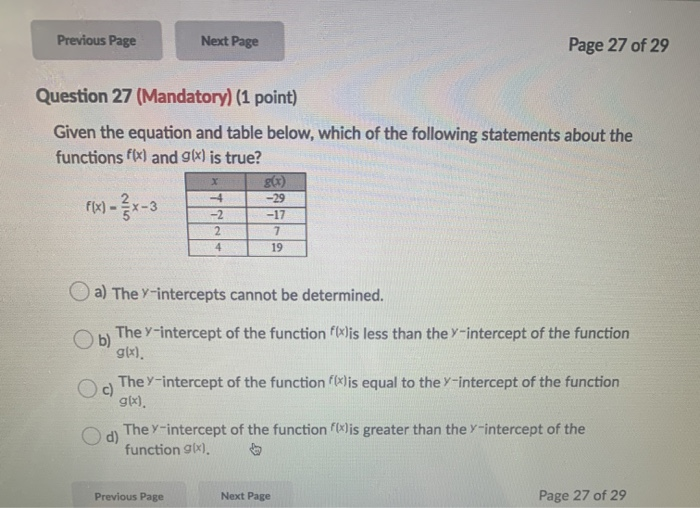



Previous Page Next Page Question 17 Mandatory 1 Chegg Com




Analyzing Tables Flashcards Quizlet
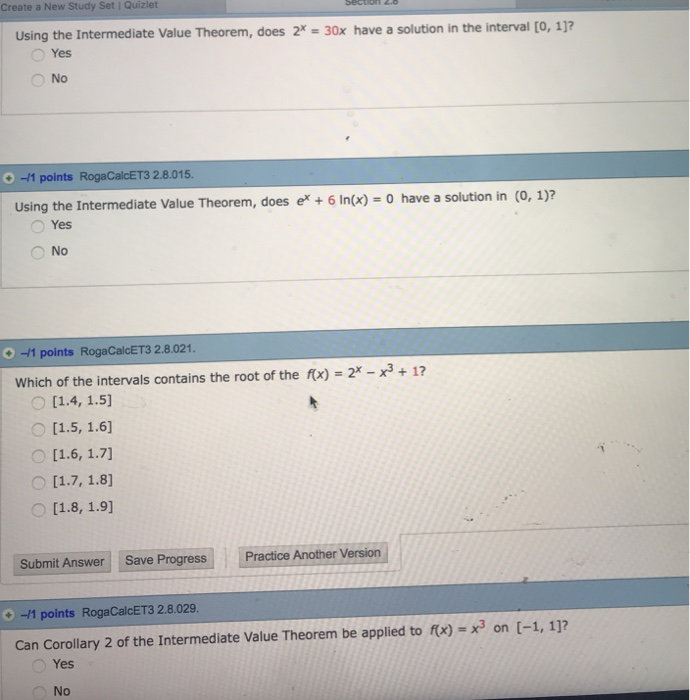



Create A New Study Set I Quizlet Using The Chegg Com




Synthesis Of Titanium Dioxide Thin Films And Its Application In Reducing Microbial Load Of Milk Biorxiv



Search Q Which Interval For The Graphed Function Contains The Local Maximum Tbm Isch




Analyzing Tables Flashcards Quizlet




Test Bank Ch 14 Simple Linear Regression Studocu




Is It Possible For A Function To Satisfy F X 0 Chegg Com




Analyzing Tables Flashcards Quizlet




Find The Power Series Centered At C 4 For F X 1 9 X And The Interval Of Convergence Youtube
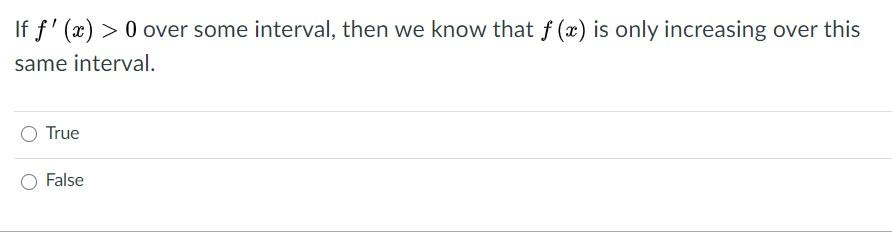



If F X 0 Over Some Interval Then We Know That F Chegg Com




Intercellular Mitochondria Transfer To Macrophages Regulates White Adipose Tissue Homeostasis And Is Impaired In Obesity Sciencedirect
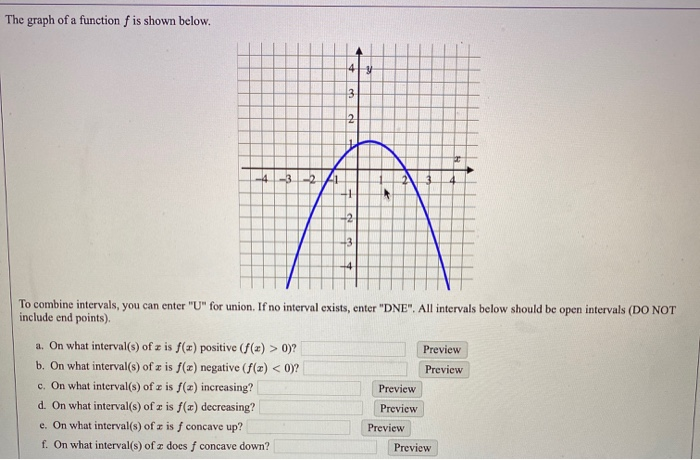



The Graph Of A Function F Is Shown Below 41 Y 3 2 4 Chegg Com
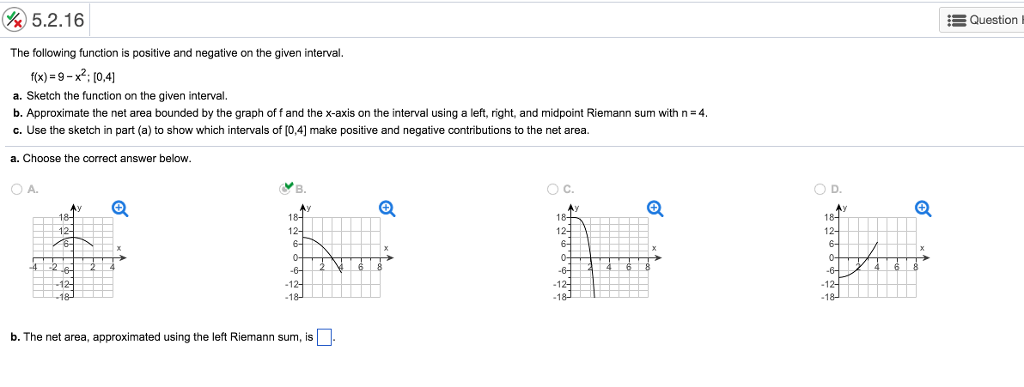



The Following Function Is Positive And Negative On Chegg Com




Analyzing Graphs Flashcards Quizlet
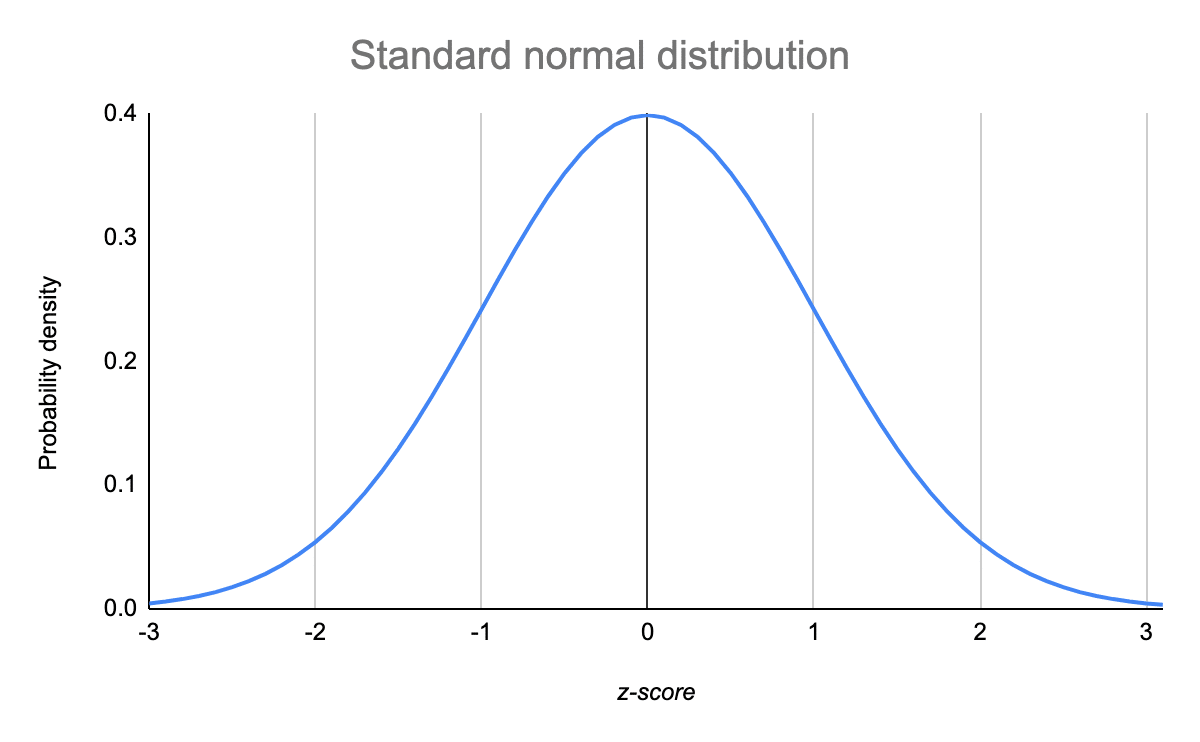



The Standard Normal Distribution Examples Explanations Uses




Which Could Be The Entire Interval Over Which The Function F X Is Negative A 8 2 B 8 Brainly Com




A 1 On What Interval S Is The Function F X 5 Chegg Com
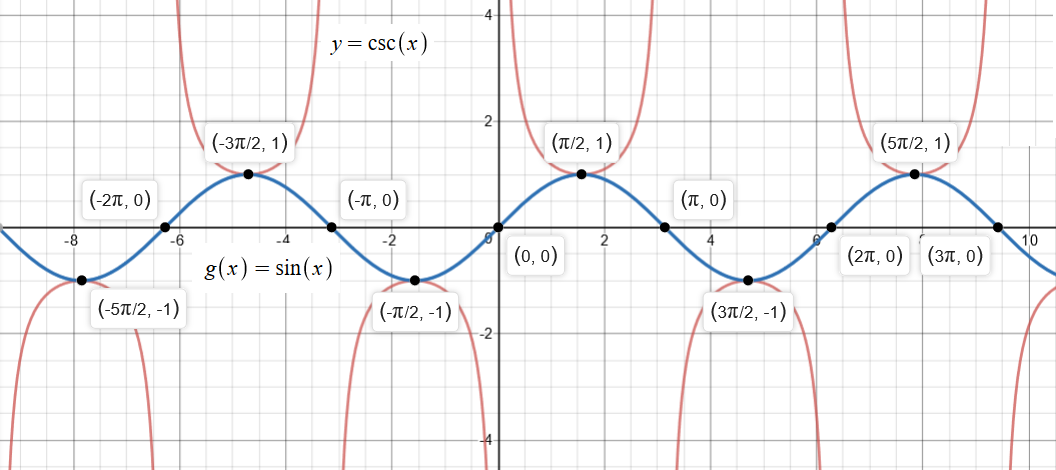



How Do You Graph Y 4csc2x Socratic



Using Quizlet




Current Status Of Immune Checkpoint Inhibition In Early Stage Nsclc Annals Of Oncology




The Rate Of Change Of A Function




Functional Magnetic Hybrid Nanomaterials For Biomedical Diagnosis And Treatment Tian 18 Wires Nanomedicine And Nanobiotechnology Wiley Online Library




Graphing Square And Cube Root Functions Video Khan Academy



Curve Sketching F X




Analyzing Graphs Flashcards Quizlet




March 17 Techiemusings




Finding Increasing Interval Given The Derivative Video Khan Academy




Which Is A Valid Prediction About The Continuous Function F X F X 0 Over The Interval 5 Brainly Com



0 件のコメント:
コメントを投稿